Атрибуция рекламных каналов: чувствительность к порядку каналов в цепочке для методов Markov chain и Shapley value

Сегодня я продолжу тему атрибуции рекламных каналов. К сожалению, эта тема очень мало описана в маркетинговой литературе (нет никаких эмпирических правил и фундаментальных исследований), а потому понять как вариация каналов повлияет на атрибуцию, без симуляции - не представляется возможным.

Итак, в прошлый раз мы рассмотрели три вида атрибуции: last_click, markov_chain и shapley_value. Также из прошлого поста мы помним, что:

• markov_chain (Цепи Маркова) - должны быть в достаточной степени чувствителны к изменению порядка каналов в цепочке;
• shapley_value (Вектор Шепли) - подход старается равномерно распределить ценность и для него порядок каналов в цепочке не играет роли.

Сегодня мы проверим на практике насколько оба метода атрибуции чувствительны к изменению порядка каналов в цепочке.

Датасет я взял из прошлого поста. Ниже пример того, как в этом датасете выглядят цепочки каналов для некоторых пользователей:

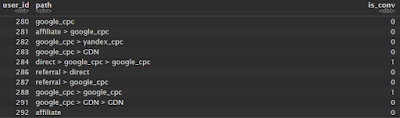Path chains.

Затем я просто реверсировал их и они начали выглядеть вот так:

Reverse Path chains.

Как мы видим на чартах выше, цепочка для пользователя 291 концептуально трансформировалась с (1) google_cpc > GDN > GDN  в (2) GDN > GDN > google_cpc.

В кейсе (1) клиент искал что-то через поиск Google и перешел на сайт с поисковой рекламы, а затем дважды переходил на сайт по дисплей рекламе с сайтов-партнеров.

В кейсе (2) все было с точностью до наоборот: клиент увидел дисплей рекламу на одном сайте-партнере Google и перешел по ней, затем (на другом?) сайте-партнере снова перешел по дисплей рекламе и лишь затем нашел сайт/продукт через рекламу в поиске Google.

Давайте рассчитаем 3 атрибуции (last_click, markov_chain, shapley_value) и посмотрим как они изменились при реверсировании цепочек.

Вначале, рассчитаем атрибуцию по оригинальной цепочке каналов.

Original path chains.

Здесь результаты идентичны тому, что мы видели в прошлом посте. 

Теперь давайте рассчитаем атрибуцию по реверсным цепочкам.

Reverse path chains.

Модель last_click моментально отреагировала на изменение порядка в цепочках.

Например, канал affiliate с 26 конверсий вырос до 110 конверсий.

Но, 

• модель markov_chain практически статична (чего мы от нее никак не ожидали);
• модель shapley_value просто не изменилась (что ожидаемо).

Я не математик и потому мои гипотезы по статичности будут весьма очевидны:

• цепочек, в которых есть конверсия (555) и при этом реверсирование меняет смысл (285) - очень мало по отношению ко всем цепочкам (12714);
• это специфика цепей Маркова первого порядка, где вероятность перехода зависит только от предыдущего канала в цепочке (а таких цепочек, как мы поняли из предыдущего пункта = 285/12714 = 2.2%);
• ошибка в реализации алгоритма в пакете ChannelAttribution.

Дальше я начал экспериментировать с параметрами функции markov_model(). Я обратил внимание в функции есть необязательное поле var_null, которое отвечает за количество заходов без конверсий для каждой цепочки.

Передав в цепь Маркова эту информацию картинка наконец-то изменилась.

Reverse path chains with nulls - total paths that do not lead to conversions.

Для удобства сравнения двух суб-методов markov_chain я сделал новую таблицу, куда добавил изначальные вероятности появления канала и вероятности конверсии.

markov_chain vs markov_chain_with_nulls.

Что мы видим?

• каналы с высокой конверсией (и низкой частотой) были пенализированы и, в тоже время,
• каналы с низкой конверсией (и высокой частотой) были вознаграждены.

И хотя абсолютные цифры в обоих суб-методах разняться, распределение весов в обеих цепях Маркова выглядят весьма схоже.

РЕЗЮМЕ:

1. Shapley_value (Вектор Шепли) не чувствителен к порядку каналов в цепочке.
2. Markov_chain (Цепи Маркова) могут быть чувствительны к порядку каналов в цепочке, но при выполнении следующих условий:
• необходимо логировать все пути - как с конверсиями так и без них;
• также, возможно, стоит использовать цепи Маркова более высоких (2-х или 3-х) порядков.

А что вы думаете об этом?

P.S.
Вектор Шепли не чувствителен к порядку каналов в цепочке. Однако давайте проверим насколько он чувствителен к вариативности самих цепочек - об этом мой следующий пост.