A/B-тестирование: последовательное семплирование как способ закончить A/B-тест раньше

Итак, недавно в закрытом комьюнити reforge поднимался вопрос про A/B-тесты и доверительные интервалы. И там, Brian Balfour (бывший VP Growth @ HubSpot), упомянул, что помимо работы с p-value важно:

• формировать сильные (читай - со значительными изменениями) гипотезы и 
• стремиться закончить успешный A/B-тест как можно раньше.

Сейчас мы не будем обсуждать первый аспект - как формировать сильные гипотезы. Обычно, в каждом конкретном случае, нужно оценивать нужды каждой группы пользователей и отдавать себе отчет в реальной ценности, которую продукт дает клиентам на этом этапе, а также насколько эта ценность четко коммуницируется.

Но второй аспект - время на завершение теста - более универсален и часто может прорабатываться без такого глубокого погружения в контекст продукта.

Начну с того, что позволю себе напомнить с чего начинается запуск A/B-теста:

1. взять цифру базовой конверсии
2. оценить ожидаемый прирост конверсии (лифт)
3. рассчитать размер минимально необходимой выборки

Здесь важно отметить два момента:

• чем выше базовая конверсия, тем меньше нужно трафика для нахождения статистически значимой разницы:
• base conversion: 2%, expected lift: 5%, sample size (per variant): 309,928 
• base conversion: 4%, expected lift: 5%, sample size (per variant): 151,776 

• чем больше ожидаемый прирост конверсии, тем еще меньше нужно трафика для нахождения статистически значимой разницы (поэтому сильная гипотеза часто = значительное изменение):
• base conversion: 2%, expected lift: 5%, sample size (per variant): 309,928
• base conversion: 2%, expected lift: 10%, sample size (per variant): 78,039

НО, на самом деле недостаточно просто посчитать размер минимально необходимой выборки. Нужно также не делать оценку теста до достижения этого объема трафика. Иначе у вас может сильно повышаться вероятность ложного срабатывания. 

При классической схеме A/B-теста мы закладываем ошибку (ложное срабатывание) в 5% случаев. Если же делать контрольные срезы до достижения минимально необходимого размера выборки, то процент ложных срабатываний может вырасти до 26,1% (в 5х раз)!

Есть ли способ закончить тест раньше и при этом не повышать частоту принятия ошибочного решения?

Есть! Это последовательное семплирование (sequential sampling). Я не буду вдаваться в математику, а просто покажу вам как таким методом можно воспользоваться.

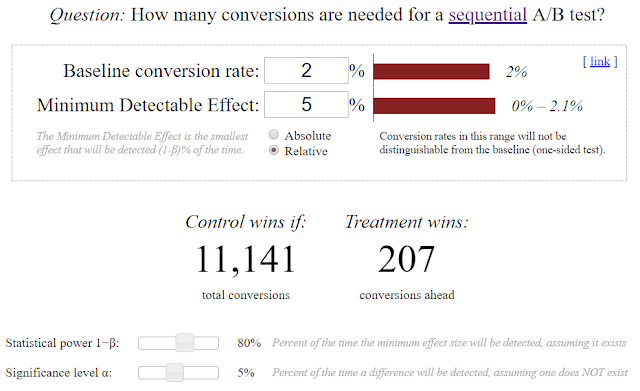
Итак, наша базовая конверсия = 2%. 

Давайте рассчитаем размер минимально необходимой выборки для проверки успешности A/B-теста:

Sample size estimation.

В классическом схеме мы ждем пока в каждой группе наберется по ~310,000 сессий и лишь затем делаем оценку успешности теста. 

Допустим через X дней у нас набралось по 310,000 сессий в каждом варианте и
Вариант 1 набрал 6,200 конверсий,
Вариант 2 набрал 6,420 конверсий.

Вставим эти данные в статистический калькулятор Chi-Squared Test и оценим результаты теста:

Chi-Squared Test.

Из расчета статистического калькулятора мы видим, что Вариант 2 выиграл и тест можно закончить. 

Отмечу, что общее количество конверсий = 6,200 + 6,420 = 12,620.

Разница между вариантами составила 220 конверсий (строго говоря, для достижения p-value < 0.05 достаточно было разницы в 218 конверсий).

Теперь давайте попробуем воспользоваться Sequential Sampling Calculator.

Как и в классической схеме A/B-теста мы в начале определяем базовую конверсию и ожидаемый прирост. 

Затем мы идем в этот специальный калькулятор и определяем стоп-конфигурацию теста:
(1) на каком объеме конверсий и (2) какой их разнице результат A/B-теста будет определен.

Sequential Test.

Допустим через Y дней у нас имеется:
Вариант 1 набрал 5,460 конверсий,
Вариант 2 набрал 5,681 конверсий.

Так как сумма конверсий = 5,460 + 5,681 = 11,141 и разница конверсий > 207, то тест можно закончить.

В результате, по сравнению с классической оценкой A/B-теста, нам удалось:

• сократить количество необходимых конверсий с 12,620 до 11,141 т.е. на 12%!
• сократить минимально необходимую разницу конверсии с 218 до 207.

Более того, автор расчетов (Evans Miller) многообещающе демонстрирует, что:

1. Чем меньшую разницу мы хотим поймать, тем большую экономию будет приносить подход последовательного семплинга (иногда экономия достигает 40%+).
2. В определенных ситуациях необходимое количество конверсий в последовательном тесте м.б. больше(!), чем при классической схеме тестирования.
3. Эмпирическое правило целесообразности использования последовательного семплинга:
   1.5 * base_conversion + lift:
1. если это число больше 36%, то - классический подход позволит закончить тест раньше, 
2. если это число меньше 36%, то - последовательное семплирование позволит закончить тест раньше.

P.S. Олег Якубенков, написал отличную статью, которая описывает проблему предварительной оценки A/B-теста (которую решает последовательный семплинг) и дал внушительный список источников описывающих детали этой проблемы. Рекомендую!